Tutorial 1: Getting Started¶

Overview¶

Welcome to FastEstimator! In this tutorial we are going to cover:

• The three main APIs of FastEstimator: Pipeline, Network, Estimator
• An image classification example
  • Pipeline
  • Network
  • Estimator
  • Training
  • Inferencing
• Related Apphub Examples

Three main APIs¶

All deep learning training workflows involve the following three essential components, each mapping to a critical API in FastEstimator.

• Data pipeline: extracts data from disk/RAM, performs transformations. -> fe.Pipeline

• Network: performs trainable and differentiable operations. -> fe.Network

• Training loop: combines the data pipeline and network in an iterative process. -> fe.Estimator

Any deep learning task can be constructed by following the 3 main steps:

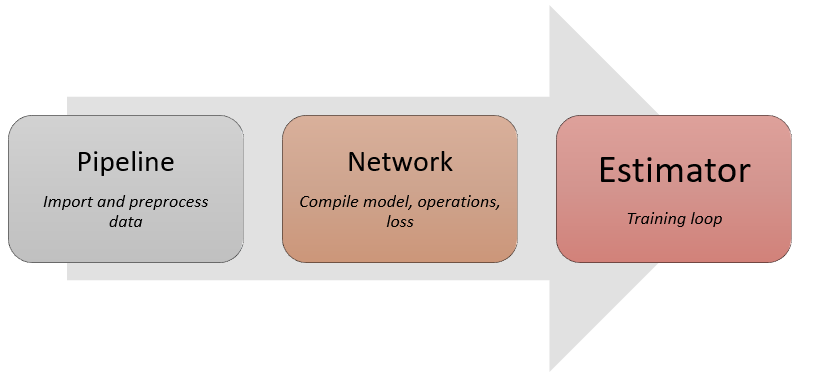
Image Classification Example¶

Step 1 - Pipeline¶

We use FastEstimator dataset API to load the MNIST dataset. Please check out Tutorial 2 for more details about the dataset API. In this case our data preprocessing involves:

1. Expand image dimension from (28,28) to (28, 28, 1) for convenience during convolution operations.
2. Rescale pixel values from [0, 255] to [0, 1].

Please check out Tutorial 3 for details about Operator and Tutorial 4 for Pipeline.

In [1]:

import fastestimator as fe
from fastestimator.dataset.data import mnist
from fastestimator.op.numpyop.univariate import ExpandDims, Minmax

train_data, eval_data = mnist.load_data()

pipeline = fe.Pipeline(train_data=train_data,
                       eval_data=eval_data,
                       batch_size=32,
                       ops=[ExpandDims(inputs="x", outputs="x"), Minmax(inputs="x", outputs="x")])

import fastestimator as fe from fastestimator.dataset.data import mnist from fastestimator.op.numpyop.univariate import ExpandDims, Minmax train_data, eval_data = mnist.load_data() pipeline = fe.Pipeline(train_data=train_data, eval_data=eval_data, batch_size=32, ops=[ExpandDims(inputs="x", outputs="x"), Minmax(inputs="x", outputs="x")])

Step 2 - Network¶

The model definition can be either from tf.keras.Model or torch.nn.Module, for more info about network definitions, check out Tutorial 5. The differentiable operations during training are listed as follows:

1. Feed the preprocessed images to the network and get prediction scores.
2. Calculate CrossEntropy (loss) between prediction scores and ground truth.
3. Update the model by minimizing CrossEntropy.

For more info about Network and its operators, check out Tutorial 6.

In [2]:

from fastestimator.architecture.tensorflow import LeNet
# from fastestimator.architecture.pytorch import LeNet  # One can also use a pytorch model

from fastestimator.op.tensorop.loss import CrossEntropy
from fastestimator.op.tensorop.model import ModelOp, UpdateOp

model = fe.build(model_fn=LeNet, optimizer_fn="adam")

network = fe.Network(ops=[
        ModelOp(model=model, inputs="x", outputs="y_pred"),
        CrossEntropy(inputs=("y_pred", "y"), outputs="ce"),
        UpdateOp(model=model, loss_name="ce") 
    ])

from fastestimator.architecture.tensorflow import LeNet # from fastestimator.architecture.pytorch import LeNet # One can also use a pytorch model from fastestimator.op.tensorop.loss import CrossEntropy from fastestimator.op.tensorop.model import ModelOp, UpdateOp model = fe.build(model_fn=LeNet, optimizer_fn="adam") network = fe.Network(ops=[ ModelOp(model=model, inputs="x", outputs="y_pred"), CrossEntropy(inputs=("y_pred", "y"), outputs="ce"), UpdateOp(model=model, loss_name="ce") ])

Step 3 - Estimator¶

We define the Estimator to connect the Network to the Pipeline, and compute accuracy as a validation metric. Please see Tutorial 7 for more about Estimator and Traces.

In [3]:

from fastestimator.trace.metric import Accuracy
from fastestimator.trace.io import BestModelSaver
import tempfile

traces = [Accuracy(true_key="y", pred_key="y_pred"),
          BestModelSaver(model=model, save_dir=tempfile.mkdtemp(), metric="accuracy", save_best_mode="max")]

estimator = fe.Estimator(pipeline=pipeline,
                         network=network,
                         epochs=2,
                         traces=traces)

from fastestimator.trace.metric import Accuracy from fastestimator.trace.io import BestModelSaver import tempfile traces = [Accuracy(true_key="y", pred_key="y_pred"), BestModelSaver(model=model, save_dir=tempfile.mkdtemp(), metric="accuracy", save_best_mode="max")] estimator = fe.Estimator(pipeline=pipeline, network=network, epochs=2, traces=traces)

Start Training¶

In [4]:

estimator.fit()

estimator.fit()

    ______           __  ______     __  _                 __            
   / ____/___ ______/ /_/ ____/____/ /_(_)___ ___  ____ _/ /_____  _____
  / /_  / __ `/ ___/ __/ __/ / ___/ __/ / __ `__ \/ __ `/ __/ __ \/ ___/
 / __/ / /_/ (__  ) /_/ /___(__  ) /_/ / / / / / / /_/ / /_/ /_/ / /    
/_/    \__,_/____/\__/_____/____/\__/_/_/ /_/ /_/\__,_/\__/\____/_/     
                                                                        

FastEstimator-Start: step: 1; num_device: 1; logging_interval: 100; 
FastEstimator-Train: step: 1; ce: 2.2944355; 
FastEstimator-Train: step: 100; ce: 0.17604804; steps/sec: 724.9; 
FastEstimator-Train: step: 200; ce: 0.6541523; steps/sec: 755.07; 
FastEstimator-Train: step: 300; ce: 0.22645846; steps/sec: 793.02; 
FastEstimator-Train: step: 400; ce: 0.1256088; steps/sec: 773.46; 
FastEstimator-Train: step: 500; ce: 0.18927144; steps/sec: 809.2; 
FastEstimator-Train: step: 600; ce: 0.07107867; steps/sec: 779.29; 
FastEstimator-Train: step: 700; ce: 0.07468874; steps/sec: 806.57; 
FastEstimator-Train: step: 800; ce: 0.23852134; steps/sec: 781.42; 
FastEstimator-Train: step: 900; ce: 0.028577618; steps/sec: 826.27; 
FastEstimator-Train: step: 1000; ce: 0.115206845; steps/sec: 776.94; 
FastEstimator-Train: step: 1100; ce: 0.07892787; steps/sec: 841.47; 
FastEstimator-Train: step: 1200; ce: 0.14857067; steps/sec: 791.73; 
FastEstimator-Train: step: 1300; ce: 0.049252644; steps/sec: 834.86; 
FastEstimator-Train: step: 1400; ce: 0.046725605; steps/sec: 799.79; 
FastEstimator-Train: step: 1500; ce: 0.06713241; steps/sec: 812.31; 
FastEstimator-Train: step: 1600; ce: 0.08489384; steps/sec: 803.99; 
FastEstimator-Train: step: 1700; ce: 0.00921803; steps/sec: 767.87; 
FastEstimator-Train: step: 1800; ce: 0.0072177458; steps/sec: 694.9; 
FastEstimator-Train: step: 1875; epoch: 1; epoch_time: 2.97 sec; 
FastEstimator-BestModelSaver: Saved model to /tmp/tmpcxa1xloj/model_best_accuracy.h5
FastEstimator-Eval: step: 1875; epoch: 1; ce: 0.06391551; accuracy: 0.9802; since_best_accuracy: 0; max_accuracy: 0.9802; 
FastEstimator-Train: step: 1900; ce: 0.006937413; steps/sec: 419.42; 
FastEstimator-Train: step: 2000; ce: 0.10369404; steps/sec: 769.67; 
FastEstimator-Train: step: 2100; ce: 0.023126157; steps/sec: 787.83; 
FastEstimator-Train: step: 2200; ce: 0.013664322; steps/sec: 807.29; 
FastEstimator-Train: step: 2300; ce: 0.15465331; steps/sec: 782.67; 
FastEstimator-Train: step: 2400; ce: 0.0059421803; steps/sec: 783.07; 
FastEstimator-Train: step: 2500; ce: 0.03436095; steps/sec: 789.81; 
FastEstimator-Train: step: 2600; ce: 0.003341827; steps/sec: 813.02; 
FastEstimator-Train: step: 2700; ce: 0.009203151; steps/sec: 779.41; 
FastEstimator-Train: step: 2800; ce: 0.0031451974; steps/sec: 818.42; 
FastEstimator-Train: step: 2900; ce: 0.03497669; steps/sec: 789.2; 
FastEstimator-Train: step: 3000; ce: 0.0043699713; steps/sec: 816.05; 
FastEstimator-Train: step: 3100; ce: 0.14205246; steps/sec: 769.89; 
FastEstimator-Train: step: 3200; ce: 0.00966863; steps/sec: 827.11; 
FastEstimator-Train: step: 3300; ce: 0.005415355; steps/sec: 780.63; 
FastEstimator-Train: step: 3400; ce: 0.027803676; steps/sec: 812.07; 
FastEstimator-Train: step: 3500; ce: 0.3876436; steps/sec: 788.85; 
FastEstimator-Train: step: 3600; ce: 0.011643453; steps/sec: 809.37; 
FastEstimator-Train: step: 3700; ce: 0.20535453; steps/sec: 794.13; 
FastEstimator-Train: step: 3750; epoch: 2; epoch_time: 2.46 sec; 
FastEstimator-BestModelSaver: Saved model to /tmp/tmpcxa1xloj/model_best_accuracy.h5
FastEstimator-Eval: step: 3750; epoch: 2; ce: 0.03874958; accuracy: 0.9867; since_best_accuracy: 0; max_accuracy: 0.9867; 
FastEstimator-Finish: step: 3750; total_time: 8.86 sec; model_lr: 0.001; 

Inferencing¶

After training, we can do inferencing on new data with Pipeline.transform and Netowork.transform. Please checkout Tutorial 8 for more details. \

In [5]:

import numpy as np

data = eval_data[0]
data = pipeline.transform(data, mode="eval")
data = network.transform(data, mode="eval")

print("Ground truth class is {}".format(data["y"][0]))
print("Predicted class is {}".format(np.argmax(data["y_pred"])))
img = fe.util.ImgData(x=data["x"])
fig = img.paint_figure()

import numpy as np data = eval_data[0] data = pipeline.transform(data, mode="eval") data = network.transform(data, mode="eval") print("Ground truth class is {}".format(data["y"][0])) print("Predicted class is {}".format(np.argmax(data["y_pred"]))) img = fe.util.ImgData(x=data["x"]) fig = img.paint_figure()

Ground truth class is 7
Predicted class is 7

Apphub Examples¶

You can find some practical examples of the concepts described here in the following FastEstimator Apphubs:

• MNIST
• DNN